用k-mer分析进行基因组调查系列：

（一）基本原理：https://yanzhongsino.github.io/2022/05/25/omics_genome.survey_01.intro/
（二）用Smudgeplot估计倍性：https://yanzhongsino.github.io/2022/12/31/omics_genome.survey_02.Smudgeplot/
（三）用jellyfish进行k-mer频数统计：https://yanzhongsino.github.io/2022/05/27/omics_genome.survey_03.jellyfish/
（四）用KMC进行k-mer频数统计：https://yanzhongsino.github.io/2022/06/05/omics_genome.survey_04.KMC/
（五）用GenomeScope评估基因组特征：https://yanzhongsino.github.io/2022/06/05/omics_genome.survey_05.GenomeScope/
（六）用GCE分步实现：https://yanzhongsino.github.io/2022/06/07/omics_genome.survey_06.GCE/
（七）用KmerGenie一步实现：https://yanzhongsino.github.io/2022/06/19/omics_genome.survey_07.KmerGenie/

【推荐】用Smudgeplot评估物种倍性后，用组合jellyfish+GenomeScope1.0做二倍体物种的基因组调查，用组合KMC+GenomeScope2.0做多倍体物种的基因组调查。

1. 基因组调查(genome survey)

1.1. 基因组调查

基因组调查(genome survey)指基因组特征评估，一般指通过k-mer分析二代测序数据，获得基因组大小(genome size)，杂合度(heterozygosity)，重复序列比例，GC含量等基因组信息的手段。

基因组调查介绍
在无参考基因组的情况下，使用中低深度的短片段测序所得的reads进行基因组调查(genome survey)，初步评估基因组特征，包括基因组大小(genome size)，杂合度(heterozygosity)，重复序列比例，GC含量等，从而为后续的基因组测序、组装和结构注释方案提供参考依据。
基因组调查的目的
基因组调查主要目的是获取两个方面的信息，一个是基因组的大小，一个是基因组复杂程度。

基因组大小(genome size)
因为测序费用是以测序量为单价计算，所以基因组越大，测序费用越高。
基因组复杂程度
基因组越复杂(杂合度越高，重复序列占比越高)，意味着测序难度和组装难度越大。

基因组调查实践

为了准确估计基因组信息，建议测序深度为50X（即预估基因组大小的50倍），最小也不低于25X。
做基因组调查和后续做基因组denovo测序需要使用同一个个体，因为有些物种个体间的基因组特征有较大的差异，且同一个个体做survey的illumina数据可用于组装。
预估基因组大小可以通过已有研究粗略判断，包括流式细胞研究，近缘种研究，也推荐植物在C值数据库网站里查询。
基因组调查(genome survey)常常使用k-mer分析来实现。

1.2. 基因组复杂程度

基因组复杂程序的判断标准包括：基因组大小，倍性，杂合度，重复序列比例，GC含量等。

一般而言，基因组越大，重复序列比例越高; GC含量异常低或异常高，重复序列比例也会很高；多倍体基因组的杂合度高于二倍体。

判断基因组复杂程度可以参考以下经验性标准：

简单基因组: 单倍体；或纯合二倍体；或杂合度低于0.5%, 且重复序列低于50%, 且GC含量在35%-65%的二倍体。
复杂基因组: 杂合度在0.5%~1.2%之间，或重复序列高于50%，或GC含量异常(<35%或>65%)的二倍体，或者多倍体。
高复杂基因组: 杂合度>1.2%；或重复序列占比大于65%。

2. k-mer分析

k-mer分析可以用在生物信息学许多方面，这篇博客的k-mer分析特指用于基因组调查的k-mer分析方法。

2.1. k-mer相关概念

monomeric unit (mer): 单体单元，单位是nt或者bp。通常用于双链核酸中的单位，100 mer DNA相当于每一条链有100nt，那么整条链就是100bp。
k-mer概念
在生物信息学中，k-mer是指包含在一段序列中的长度为k的子串。一段长度为L的核酸序列，以一个碱基为步长滑动，一共可以生成(L-K+1)个k-mers，另外还可以用这段核酸的反向互补序列再生成一次k-mer。

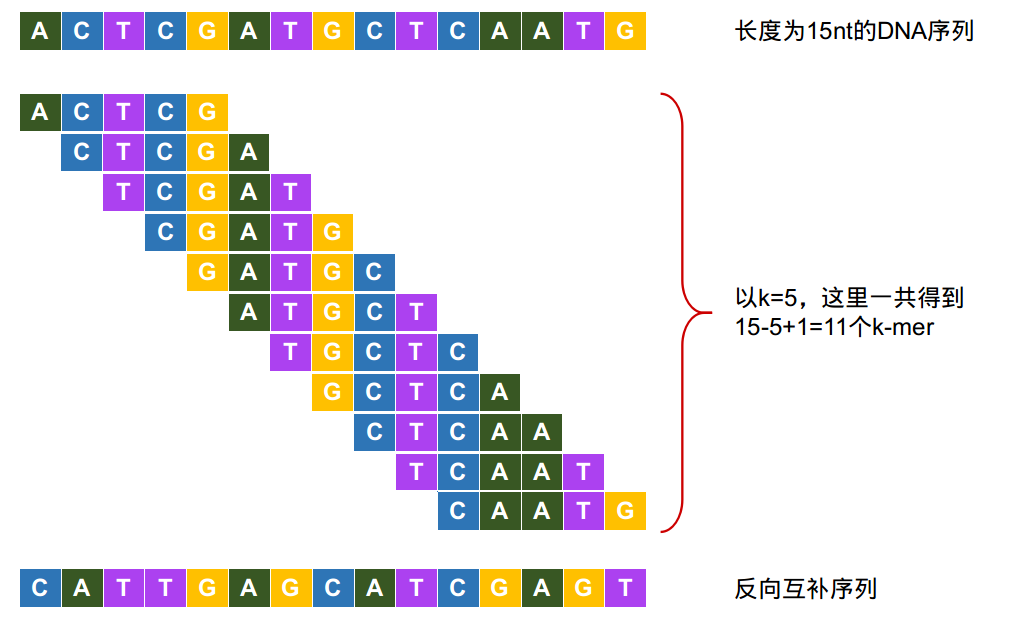
Figure 1. k-mer示例，图片来源： k-mer与基因组

2.2. k-mer分析步骤

通过切割二代测序的reads为k-mers
统计k-mer的总数和每一种k-mer的频数
绘制k-mer的频数分布图
根据k-mer的频数分布的主峰峰值判定k-mer的期望深度(即主峰对应的k-mer频数)。
根据k-mer的期望深度和k-mer的总数估计基因组大小。
根据低频k-mer估计数据错误率，并修正基因组大小的估计。
根据k-mer的其他峰估计k-mer的杂合度和重复序列比例。

2.3. k-mer原理

k-mer分析应用的前提假设是测序的reads是随机分布在基因组上的。

首先定义几个变量，方便解释原理：

基因组大小：G
read读长：L
reads总条数：n
k-mer长度：K

2.3.1. 碱基深度分布

单条read测序覆盖到某一个碱基的概率：$L/G$。
因为L/G很小，n很大，每个碱基覆盖深度服从泊松分布。
则每个碱基的覆盖深度的期望为：$d=(L/G)*n$。

2.3.2. k-mer深度分布

一个大小为G的基因组可以产生的k-mer种类约为G。

假设一个基因组产生的K都是unique的，从一个大小为G的基因组可以得到$(G-K+1)$种不同的k-mer。
一般而言，基因组大小G在几百Mb或者Gb为单位，远大于K和1，所以K和1可以忽略不计，约等于G种k-mer。

单条read测序完全覆盖某种k-mer的概率：$(L-K+1)/G$。

k-mer种类的总数约为G
单条read能产生的k-mer种类数量为$(L-K+1)$。
假设read随机分布在基因组上，单条read测序完全覆盖某种k-mer的概率就为：$(L-K+1)/G$。

同样因为$(L-K+1)/G$很小，n很大，每种k-mer的覆盖深度服从泊松分布。
每种k-mer的覆盖深度的期望为：$D=((L-K+1)/G)*n$。
由此可以得到，基因组大小为：$G=(L-K+1)*n/D$。

2.3.3. 基因组大小

计算总k-mer个数N和k-mer期望深度D

对测序reads进行k-mer分割，获得总k-mer个数N。
统计所有分割的k-mer，绘制频数分布图。
理想情况下(不考虑测序错误、序列重复性和杂合序列的条件下)，k-mer的频数分布遵循泊松分布，可以将频数分布峰值的k-mer频数作为k-mer的期望深度D。

通过下面公式可知，基因组大小$G=N/D$。

k-mer的总数量$N=(L-K+1)*n$
k-mer的期望深度$D=((L-K+1)/G)*n$

只要通过k-mer分析计算得到k-mer的总数量N和k-mer的期望深度D，则可以算出基因组大小G。

2.3.4. 基因组调查

在不考虑测序错误、序列重复性和杂合序列的条件下，k-mer的深度分布遵循泊松分布。但实际情况是三者都存在，所以需要计算错误率，重复序列占比和杂合度，并根据计算结果修正对基因组大小的估计。

2.3.4.1. 错误率

测序错误：一般认为低频k-mer(K=1,2…)是测序错误引起的，去除低频k-mer并计算错误率以修正基因组大小的估计。
一般把拐点前的低频k-mer当作错误去除。

2.3.4.2. 重复序列占比

基因组中存在的重复序列会使对应的k-mer频数高于k-mer期望深度D。
在k-mer频数分布图中重复序列对应的k-mer会表现为频数大于主峰的一个重复峰。
根据主峰右侧的重复峰可以估计基因组的重复序列比例。
- 通过模型计算一个阈值，比如阈值为1.6倍主峰，理论上单拷贝序列(非重复序列)出现在1.6倍主峰右边的概率很低，可以把1.6倍主峰之后的看作重复k-mer。
- 统计重复k-mer的总数量m，从而可以算出：重复序列的大小R=重复k-mer的总数量m/k-mer的期望深度D。
- R/G即为重复序列占基因组的比例。

2.3.4.3. 杂合度

基因组中存在的杂合序列会对应两种类型的k-mer，并使得这些k-mer频数低于k-mer期望深度D。
假设两种k-mer数量大致相等，在k-mer频数分布图中杂合序列对应的k-mer会表现为频数约为主峰一半的一个杂合峰。
根据主峰左侧的杂合峰可以估计基因组的杂合度。
- 假设基因组中的杂合率为 h（每个碱基为杂合点的概率）,一个k-mer是纯合k-mer的概率为 $P1 = (1-h)^k$, 则是杂合的概率 $P2 = 1-P1 = 1-(1-h)^k$。
- 假设产生的k-mer种类的总数为M，其中属于单拷贝序列(非重复序列)的k-mer种类。
- 在二倍体中，单拷贝序列(非重复序列)的同源区域，会产生 U×P2 的杂合k-mer，这个数是可以通过计算得到的：只要统计非重复k-mer的总数 M , M-U即为产生的杂合k-mer数。则 $M-U = U×P2 = U×(1-(1-h)^k)$。
- 通过计算，即可通过M和U的值得到基因组的杂合率h。

在实际应用过程中，估计了基因组的错误率、杂合度和重复序列比例后，重新修正基因组大小的估计，从而得到基因组调查的结果。

Figure 2. k-mer分析(GenomeScope)结果示例

2.4. k-mer用途

许多分析都会用到k-mer的处理方法，把测序得到的reads通过截取k-mer后用于分析。

比如评估基因组特征，组装基因组，物种样品污染评估等。评估基因组特征(genome survey)包括评估基因组大小(size)，杂合度，重复序列比例等。

组装基因组
组装基因组使用k-mer的目的主要是去除低频率的k-mer以提高组装结果准确性。
评估基因组大小(size)
在不考虑测序错误、序列重复性的条件下，k-mer的深度分布遵循泊松分布，可以将深度分布曲线的峰值作为期望测序深度。

在k-mer原理部分解释了用k-mer评估基因组大小的公式：

$$基因组大小G=总k-mer数量N/k-mer期望深度D$$

评估基因组杂合度
根据k-mer频数分布图的杂合峰，可以估计基因组的杂合度。
评估基因组重复序列比例
根据k-mer频数分布图的重复峰，可以估计基因组的重复序列比例。
评估物种样品污染
根据k-mer频数分布图，可以评估测序样品污染情况。

如果k-mer频数分布图出现两个明显的峰，但两个峰的横坐标又不是二倍关系，那就可能是DNA污染导致的。
因为一个物种的杂合峰的频数约为主峰的一半，重复峰的频数约为主峰的两倍。
如果DNA中存在两个物种的样品(即有污染)，期望会出现对应的两个峰，且两个峰的横坐标之间也非两倍的关系，由此可以初步判定该测序样本存在污染。
至于具体是因为什么物种造成污染，则可以通过blast比对nr库进行简单的判断。

除了通过k-mer频数分布评估DNA样品的污染程度外，还可以通过GC含量分布图判断，查看图中是否存在多个密度集中的类群。

2.5. k-mer的优势和局限

增加准确率

二代测序的准确率已达到99.9%，但测序量非常大时，错误碱基的绝对数量(比如10亿碱基里错误碱基数量会达到1000万个)还是会对分析有很大的影响。
由于测序错误具有随机性，通过将reads切割产生的k-mer中，测序错误生成的k-mer绝大多数都是测序物种中不存在的k-mer，因此都只出现1次(或很少的几次)，要是将这些低频的k-mer去掉，就有较大可能去除测序错误，从而使得分析(基因组调查，组装基因组)结果更可靠。

不适用过于复杂的基因组

k-mer分析适用于分析唯一主峰区域所占比例较大的基因组。
当基因组杂合非常高或者重复序列比例非常大时，其影响可能导致无法通过k-mer分析正确估计基因组大小。

2.6. k-mer的选择

2.6.1. k-mer的大小选择

K应该足够大到k-mer可以映射到基因组的唯一位置。
太大的k-mer会降低去除低频k-mer代表的错误碱基的概率(增加错误率)，也会降低k-mer深度(使得k-mer频数分布的峰不明显)，而且大的k-mer会增加计算资源的使用。
基因组调查一般选17，21比较常见。

2.6.2. 选择k-mer的考虑

k-mer只能是奇数？

把k-mer设置成奇数是为了防止通过k-mer组装时，正反链混淆。
偶数的k-mer的反向互补序列常常与自身一样，从而组装k-mer时会混淆正反链的组装，奇数的k-mer就不存在这个问题。

k-mer的长度代表了可能存在的k-mer种类的数量(4的K次方)，越长的k-mer片段映射的物种特异性越强。基因组越大，需要的k-mer越长。
当基因组中有较多重复序列时，可以用较大的k-mer来跨过高重复的区域，从而获得更加准确及完整的基因组草图；
由于reads上的碱基错误率的存在，选择较长的k-mer会带来较高的错误率，这也可以加大测序深度来弥补。
如果是用于组装基因组，为了得到更加完整的基因组，要尽可能使用较长的k-mer用于组装。

3. k-mer分析软件

3.1. k-mer分析软件简介

k-mer分析分为k-mer频数统计和基因组特征评估两步。此外，Smudgeplot还可以用k-mer分析评估物种的倍性。

jellyfish

jellyfish可以实现第一步k-mer频数统计。
特点是使用Hash表存储数据，能多线程运行；速度快，内存消耗小。

KMC可以实现第一步k-mer频数统计。

GenomeScope

GenomeScope可以实现第二步，利用k-mer频数统计结果进行基因组特征评估。
1.0版本用于二倍体物种，2.0版本用于多倍体物种。

KAT(The k-mer Analysis Toolkit)

KAT(The k-mer Analysis Toolkit)可以实现k-mer频数统计和基因组特征评估两步。
包含多个工具来帮助用户通过使用k-mer对测序数据进行简单分析，如组装完整性、测序错误、是否有污染等。

GCE可以分别实现k-mer频数统计和基因组特征评估两步。

KmerGenie

KmerGenie可以同时实现k-mer频数统计和基因组特征评估两步。
最大优点在于可以实现在多个预设k-mer下的自动分析，除了进行常规的k-mer频数统计之外，还能够基于不同k-mer自动计算基因组大小，并为基因组组装评估一个最佳组装k-mer数值作为备选。

3.2. 一些使用软件的经验总结

【推荐】用Smudgeplot评估物种倍性后，用组合jellyfish+GenomeScope1.0做二倍体物种的基因组调查，用组合KMC+GenomeScope2.0做多倍体物种的基因组调查。
k-mer长度常用17/21。
软件KmerGenie，GCE和jellyfish获取的频数分布表，都可用于软件genomescope和GCE第二步骤的分析。
由于GCE第一步骤支持的最大k-mer频数为255，大于255的数据被合并；而jellyfish统计到10000行，预估结果会更为准确。
GenomeScope对于高重复序列的基因组统计的基因组大小会偏小，建议max kmer coverage设置大一点，大于等于10000。
有些软件有另一个参数需注意和设定，单倍体模式还是杂合模式，可以两种模式都分析，查看差别。
实践经验发现，k-mer值设置得越高，估计出来的基因组size会越大；
另外，在jellyfish里的jellyfish histo统计频数分布时，用参数-h 10000把统计上限调高，以及在GenomeScope阶段，Max kmer coverage设置的大一些(即统计进的kmer数量越多)，估算出来的基因组大小也会略大一些。

4. references

wiki_k-mer: https://en.wikipedia.org/wiki/k-mer
genome survey：https://xuzhougeng.top/archives/genome-survey-using-kmers
xuzhougeng’s blog：https://www.jianshu.com/p/85de8f025899
k-mer与基因组组装：https://cloud.tencent.com/developer/article/1613847
k-mer分析和原理：https://www.bbsmax.com/A/lk5aQMxP51/
jellyfish paper：https://academic.oup.com/bioinformatics/article/27/6/764/234905?login=true
jellyfish github：https://github.com/gmarcais/Jellyfish
GenomeScope1.0 github：https://github.com/schatzlab/genomescope
KAT github：https://github.com/TGAC/KAT
GCE github：https://github.com/fanagislab/GCE

欢迎关注微信公众号：生信技工
公众号主要分享生信分析、生信软件、基因组学、转录组学、植物进化、生物学概念等相关内容，包括生物信息学工具的基本原理、操作步骤和学习心得。